Vfrdtyky

In geometry, a solid angle (symbol: $Ω$ ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle from that point.

In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a steradian (symbol: sr). One steradian corresponds to one unit of area on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, $4pi$ . Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds.

A small object nearby may subtend the same solid angle as a larger object farther away. For example, although the Moon is much smaller than the Sun, it is also much closer to Earth. Indeed, as viewed from any point on Earth, both objects have approximately the same solid angle as well as apparent size. This is evident during a solar eclipse.

Definition and properties

An object's solid angle in steradians is equal to the area of the segment of a unit sphere, centered at the apex, that the object covers. A solid angle in steradians equals the area of a segment of a unit sphere in the same way a planar angle in radians equals the length of an arc of a unit circle; therefore, just like a planar angle in radians is the ratio of the length of a circular arc to its radius, a solid angle in steradians is the following ratio:

{displaystyle Omega ={frac {A}{r^{2}}}}

where A is the spherical surface area and r is the radius of the considered sphere.

Solid angles are often used in physics, in particular astrophysics. The solid angle of an object that is very far away is roughly proportional to the ratio of area to squared distance. Here "area" means the area of the object when projected along the viewing direction.

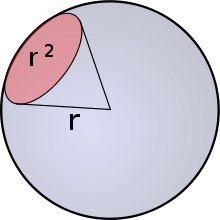
Any area on a sphere which is equal in area to the square of its radius, when observed from its center, subtends precisely one steradian.

The solid angle of a sphere measured from any point in its interior is 4 $π$ sr, and the solid angle subtended at the center of a cube by one of its faces is one-sixth of that, or 2 $π$ /3 sr. Solid angles can also be measured in square degrees (1 sr = (180/ $π$ )² square degrees), in square minutes and square seconds, or in fractions of the sphere (1 sr = 1/4 $π$ fractional area), also known as spat (1 sp = 4 $π$ sr).

In spherical coordinates there is a formula for the differential,

dOmega =sin theta ,dtheta ,dvarphi

where $θ$ is the colatitude (angle from the North pole) and $φ$ is the longitude.

The solid angle for an arbitrary oriented surface S subtended at a point P is equal to the solid angle of the projection of the surface S to the unit sphere with center P, which can be calculated as the surface integral:

{displaystyle Omega =iint limits _{S}{frac {{hat {r}}cdot {hat {n}},dSigma }{r^{2}}} =iint limits _{S}sin theta ,dtheta ,dvarphi }

where ${displaystyle {hat {r}}={tfrac {vec {r}}{r}}}$ is the unit vector corresponding to ${vec {r}}$ , the position vector of an infinitesimal area of surface $d Σ$ with respect to point P, and where ${hat {n}}$ represents the unit normal vector to $d Σ$ . Even if the projection on the unit sphere to the surface S is not isomorphic, the multiple folds are correctly considered according to the surface orientation described by the sign of the scalar product ${hat {r}}cdot {hat {n}}$ .

Thus one can approximate the solid angle subtended by a small facet having flat surface area $d Σ$ , orientation ${hat {n}}$ , and distance $r$ from the viewer as:

{displaystyle dOmega =4pi left({frac {dSigma }{A}}right),({hat {r}}cdot {hat {n}})}

where the surface area of a sphere is $A = 4π r 2$ .

Practical applications

Defining luminous intensity and luminance, and the correspondent radiometric quantities radiant intensity and radiance

Calculating spherical excess $E$ of a spherical triangle

The calculation of potentials by using the boundary element method (BEM)

Evaluating the size of ligands in metal complexes, see ligand cone angle

Calculating the electric field and magnetic field strength around charge distributions

Deriving Gauss's Law

Calculating emissive power and irradiation in heat transfer

Calculating cross sections in Rutherford scattering

Calculating cross sections in Raman scattering

The solid angle of the acceptance cone of the optical fiber

Solid angles for common objects

Cone, spherical cap, hemisphere

Section of cone (1) and spherical cap (2) inside a sphere. In this figure

θ = A / 2

and

r = 1

.

The solid angle of a cone with its apex at the apex of the solid angle, and with apex angle 2 $θ$ , is the area of a spherical cap on a unit sphere

{displaystyle Omega =2pi left(1-cos {theta }right) =4pi sin ^{2}left({frac {theta }{2}}right) }

For small $θ$ such that $cos θ \approx 1 - θ 2 /2$ , this reduces to the area of a circle $π θ 2$ .

The above is found by computing the following double integral using the unit surface element in spherical coordinates:

{displaystyle int _{0}^{2pi }int _{0}^{theta }sin theta ',dtheta ',dphi =2pi int _{0}^{theta }sin theta ',dtheta ' =2pi left[-cos theta 'right]_{0}^{theta } =2pi left(1-cos theta right) }

This formula can also be derived without the use of calculus. Over 2200 years ago Archimedes proved that the surface area of a spherical cap is always equal to the area of a circle whose radius equals the distance from the rim of the spherical cap to the point where the cap's axis of symmetry intersects the cap.^[1] In the diagram this radius is given as:

{displaystyle 2rsin {frac {theta }{2}}}

Hence for a unit sphere the solid angle of the spherical cap is given as:

{displaystyle Omega =4pi sin ^{2}left({frac {theta }{2}}right)=2pi left(1-cos {theta }right) }

When $θ$ = $π$ /2, the spherical cap becomes a hemisphere having a solid angle 2 $π$ .

The solid angle of the complement of the cone (picture a melon with the cone cut out) is clearly:

{displaystyle 4pi -Omega =2pi left(1+cos {theta }right)=4pi cos ^{2}left({frac {theta }{2}}right)}

This is also the solid angle of the part of the celestial sphere that a Terran astronomical observer positioned at latitude $θ$ can see as the earth rotates. At the equator you see all of the celestial sphere, at either pole only one half.

The solid angle subtended by a segment of a spherical cap cut by a plane at angle $γ$ from the cone's axis and passing through the cone's apex can be calculated by the formula:^[2]

Omega =2left[arccos left({frac {sin gamma }{sin theta }}right)-cos theta arccos left({frac {tan gamma }{tan theta }}right)right]

For example, if $γ$ =- $θ$ , then the formula reduces to the spherical cap formula above: the first term becomes $π$ , and the second $π$ cos $θ$ .

Tetrahedron

Let OABC be the vertices of a tetrahedron with an origin at O subtended by the triangular face ABC where ${vec {a}} ,,{vec {b}} ,,{vec {c}}$ are the vector positions of the vertices A, B and C. Define the vertex angle $θ a$ to be the angle BOC and define $θ b$ , $θ c$ correspondingly. Let $φ ab$ be the dihedral angle between the planes that contain the tetrahedral faces OAC and OBC and define $φ ac$ , $φ bc$ correspondingly. The solid angle $Ω$ subtended by the triangular surface ABC is given by

Omega =left(phi _{ab}+phi _{bc}+phi _{ac}right) -pi

This follows from the theory of spherical excess and it leads to the fact that there is an analogous theorem to the theorem that "The sum of internal angles of a planar triangle is equal to $π$ ", for the sum of the four internal solid angles of a tetrahedron as follows:

sum _{i=1}^{4}Omega _{i}=2sum _{i=1}^{6}phi _{i} -4pi

where $φ i$ ranges over all six of the dihedral angles between any two planes that contain the tetrahedral faces OAB, OAC, OBC and ABC.^[3]

A useful formula for calculating the solid angle $Ω$ subtended by the triangular surface ABC where ${vec {a}} ,,{vec {b}} ,,{vec {c}}$ are the vector positions of the vertices A, B and C has been given by Oosterom and Strackee ^[4] (although the result was known earlier by Euler and Lagrange^[5]):

tan left({frac {1}{2}}Omega right)={frac {left|{vec {a}} {vec {b}} {vec {c}}right|}{abc+left({vec {a}}cdot {vec {b}}right)c+left({vec {a}}cdot {vec {c}}right)b+left({vec {b}}cdot {vec {c}}right)a}}

where

left|{vec {a}} {vec {b}} {vec {c}}right|={vec {a}}cdot ({vec {b}}times {vec {c}})

denotes the scalar triple product of the three vectors;

{vec {a}}

is the vector representation of point A, while

a

is the magnitude of that vector (the origin-point distance)

{vec {a}}cdot {vec {b}}

denotes the scalar product.

When implementing the above equation care must be taken with the atan function to avoid negative or incorrect solid angles. One source of potential errors is that the scalar triple product can be negative if $a$ , $b$ , $c$ have the wrong winding. Computing abs(det) is a sufficient solution since no other portion of the equation depends on the winding. The other pitfall arises when the scalar triple product is positive but the divisor is negative. In this case atan returns a negative value that must be increased by $π$ .

Another useful formula for calculating the solid angle of the tetrahedron at the origin O that is purely a function of the vertex angles $θ a$ , $θ b$ , $θ c$ is given by L'Huilier's theorem^[6]^[7] as

tan left({frac {1}{4}}Omega right)={sqrt {tan left({frac {theta _{s}}{2}}right)tan left({frac {theta _{s}-theta _{a}}{2}}right)tan left({frac {theta _{s}-theta _{b}}{2}}right)tan left({frac {theta _{s}-theta _{c}}{2}}right)}}

where

theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}}

Pyramid

The solid angle of a four-sided right rectangular pyramid with apex angles $a$ and $b$ (dihedral angles measured to the opposite side faces of the pyramid) is

Omega =4arcsin left(sin left({a over 2}right)sin left({b over 2}right)right)

If both the side lengths ( $α$ and $β$ ) of the base of the pyramid and the distance ( $d$ ) from the center of the base rectangle to the apex of the pyramid (the center of the sphere) are known, then the above equation can be manipulated to give

Omega =4arctan {frac {alpha beta }{2d{sqrt {4d^{2}+alpha ^{2}+beta ^{2}}}}}

The solid angle of a right $n$ -gonal pyramid, where the pyramid base is a regular $n$ -sided polygon of circumradius $r$ , with a
pyramid height $h$ is

Omega =2pi -2narctan left({frac {tan left({pi over n}right)}{sqrt {1+{r^{2} over h^{2}}}}}right)

The solid angle of an arbitrary pyramid with an $n$ -sided base defined by the sequence of unit vectors representing edges ${s 1, s 2}, ... s n$ can be efficiently computed by:^[2]

Omega =2pi -arg prod _{j=1}^{n}left(left(s_{j-1}s_{j}right)left(s_{j}s_{j+1}right)-left(s_{j-1}s_{j+1}right)+ileft[s_{j-1}s_{j}s_{j+1}right]right)

where parentheses (* *) is a scalar product and square brackets [* * *] is a scalar triple product, and $i$ is an imaginary unit. Indices are cycled: $s 0 = s n$ and $s 1 = s n + 1$ .

Latitude-longitude rectangle

The solid angle of a latitude-longitude rectangle on a globe is

{displaystyle left(sin phi _{mathrm {N} }-sin phi _{mathrm {S} }right)left(theta _{mathrm {E} }-theta _{mathrm {W} },!right);mathrm {sr} }

,

where $φ N$ and $φ S$ are north and south lines of latitude (measured from the equator in radians with angle increasing northward), and $θ E$ and $θ W$ are east and west lines of longitude (where the angle in radians increases eastward).^[8] Mathematically, this represents an arc of angle $φ N - φ S$ swept around a sphere by $θ E - θ W$ radians. When longitude spans 2 $π$ radians and latitude spans $π$ radians, the solid angle is that of a sphere.

A latitude-longitude rectangle should not be confused with the solid angle of a rectangular pyramid. All four sides of a rectangular pyramid intersect the sphere's surface in great circle arcs. With a latitude-longitude rectangle, only lines of longitude are great circle arcs; lines of latitude are not.

Sun and Moon

The Sun is seen from Earth at an average angular diameter of 0.5334 degrees or 9.310×10⁻³ radians. The Moon is seen from Earth at an average angular diameter of 9.22×10⁻³ radians. We can substitute these into the equation given above for the solid angle subtended by a cone with apex angle $2θ$ :

{displaystyle Omega =2pi left(1-cos {theta }right)}

The resulting value for the Sun is 6.807×10⁻⁵ steradians. The resulting value for the Moon is 6.67×10⁻⁵ steradians. In terms of the total celestial sphere, the Sun and the Moon subtend fractional areas of 0.000542% (Sun) and 0.000531% (Moon). On average, the Sun is larger in the sky than the Moon even though it is much, much farther away.

Solid angles in arbitrary dimensions

The solid angle subtended by the complete ( $d - 1$ )-dimensional spherical surface of the unit sphere in $d$ -dimensional Euclidean space can be defined in any number of dimensions $d$ . One often needs this solid angle factor in calculations with spherical symmetry. It is given by the formula

Omega _{d}={frac {2pi ^{frac {d}{2}}}{Gamma left({frac {d}{2}}right)}}

where $Γ$ is the gamma function. When $d$ is an integer, the gamma function can be computed explicitly.^[9] It follows that

Omega _{d}={begin{cases}{frac {1}{left({frac {d}{2}}-1right)!}}2pi ^{frac {d}{2}} &d{text{ even}}\{frac {left({frac {1}{2}}left(d-1right)right)!}{(d-1)!}}2^{d}pi ^{{frac {1}{2}}(d-1)} &d{text{ odd}}end{cases}}

This gives the expected results of 4 $π$ steradians for the 3D sphere bounded by a surface of area $4π r 2$ and 2 $π$ radians for the 2D circle bounded by a circumference of length $2π r$ . It also gives the slightly less obvious 2 for the 1D case, in which the origin-centered 1D "sphere" is the interval $[ - r, r]$ and this is bounded by two limiting points.

The counterpart to the vector formula in arbitrary dimension was derived by Aomoto
^[10]^[11]
and independently by Ribando.^[12] It expresses them as an infinite multivariate Taylor series:

{displaystyle Omega =Omega _{d}{frac {|operatorname {det} (V)|}{(4pi )^{d/2}}}sum _{ain mathbb {N} ^{binom {d}{2}}}left[{frac {(-2)^{sum _{i<j}a_{ij}}}{prod _{i<j}a_{ij}!}}prod _{i}Gamma left({frac {1+sum _{mneq i}a_{im}}{2}}right)right]alpha ^{a}.}

Given $d$ unit vectors ${displaystyle {vec {v_{i}}}}$ defining the angle, let $V$ denote the matrix formed by combining them so the $i$ th column is ${displaystyle {vec {v_{i}}},}$ and ${displaystyle alpha _{ij}={vec {v_{i}}}cdot {vec {v_{j}}}.}$ Where this series converges, it converges to the solid angle defined by the vectors.

References

^ "Archimedes on Spheres and Cylinders". Math Pages. 2015..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}

^ ^a^b Mazonka, Oleg (2012). "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396 [math.MG].

^ Hopf, Heinz (1940). "Selected Chapters of Geometry" (PDF). ETH Zurich: 1–2.

^ Van Oosterom, A; Strackee, J (1983). "The Solid Angle of a Plane Triangle". IEEE Trans. Biomed. Eng. BME-30 (2): 125–126. doi:10.1109/TBME.1983.325207.

^ Eriksson, Folke (1990). "On the measure of solid angles". Math. Mag. 63 (3): 184–187. doi:10.2307/2691141. JSTOR 2691141.

^ "L'Huilier's Theorem – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

^ "Spherical Excess – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

^ "Area of a Latitude-Longitude Rectangle". The Math Forum @ Drexel. 2003.

^ Jackson, FM (1993). "Polytopes in Euclidean n-space". Bulletin of the Institute of Mathematics and its Applications. 29 (11/12): 172–174.

^ Aomoto, Kazuhiko (1977). "Analytic structure of Schläfli function". Nagoya Math. J. 68: 1–16. doi:10.1017/s0027763000017839.

^ Beck, M.; Robins, S.; Sam, S. V. (2010). "Positivity theorems for solid-angle polynomials". Contributions to Algebra and Geometry. 51 (2): 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.

^ Ribando, Jason M. (2006). "Measuring Solid Angles Beyond Dimension Three". Discrete & Computational Geometry. 36 (3): 479–487. doi:10.1007/s00454-006-1253-4.

External links

Arthur P. Norton, A Star Atlas, Gall and Inglis, Edinburgh, 1969.

M. G. Kendall, A Course in the Geometry of N Dimensions, No. 8 of Griffin's Statistical Monographs & Courses, ed. M. G. Kendall, Charles Griffin & Co. Ltd, London, 1961

Weisstein, Eric W. "Solid Angle". MathWorld.

[1] "Archimedes on Spheres and Cylinders". Math Pages. 2015..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}

[Mazonka-2] Mazonka, Oleg (2012). "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396 [math.MG].

[3] Hopf, Heinz (1940). "Selected Chapters of Geometry" (PDF). ETH Zurich: 1–2.

[4] Van Oosterom, A; Strackee, J (1983). "The Solid Angle of a Plane Triangle". IEEE Trans. Biomed. Eng. BME-30 (2): 125–126. doi:10.1109/TBME.1983.325207.

[5] Eriksson, Folke (1990). "On the measure of solid angles". Math. Mag. 63 (3): 184–187. doi:10.2307/2691141. JSTOR 2691141.

[6] "L'Huilier's Theorem – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

[7] "Spherical Excess – from Wolfram MathWorld". Mathworld.wolfram.com. 2015-10-19. Retrieved 2015-10-19.

[8] "Area of a Latitude-Longitude Rectangle". The Math Forum @ Drexel. 2003.

[9] Jackson, FM (1993). "Polytopes in Euclidean n-space". Bulletin of the Institute of Mathematics and its Applications. 29 (11/12): 172–174.

[10] Aomoto, Kazuhiko (1977). "Analytic structure of Schläfli function". Nagoya Math. J. 68: 1–16. doi:10.1017/s0027763000017839.

[11] Beck, M.; Robins, S.; Sam, S. V. (2010). "Positivity theorems for solid-angle polynomials". Contributions to Algebra and Geometry. 51 (2): 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.

[12] Ribando, Jason M. (2006). "Measuring Solid Angles Beyond Dimension Three". Discrete & Computational Geometry. 36 (3): 479–487. doi:10.1007/s00454-006-1253-4.

搜尋此網誌

Vfrdtyky

Solid angle

Contents

Definition and properties

Practical applications

Solid angles for common objects

Cone, spherical cap, hemisphere

Tetrahedron

Pyramid

Latitude-longitude rectangle

Sun and Moon

Solid angles in arbitrary dimensions

References

Further reading

External links

Popular posts from this blog

Bressuire

Vorschmack

Quarantine