Vfrdtyky

In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle. (The magnetic moment, also called magnetic dipole moment, is a measure of the strength of a magnetic source.)

The "Dirac" magnetic moment, corresponding to tree-level Feynman diagrams (which can be thought of as the classical result), can be calculated from the Dirac equation. It is usually expressed in terms of the g-factor; the Dirac equation predicts g = 2. For particles such as the electron, this classical result differs from the observed value by a small fraction of a percent. The difference is the anomalous magnetic moment, denoted a and defined as

a=g−22{displaystyle a={frac {g-2}{2}}}

Electron

One-loop correction to the fermion's magnetic dipole moment.

The one-loop contribution to the anomalous magnetic moment—corresponding to the first and largest quantum mechanical correction—of the electron is found by calculating the vertex function shown in the adjacent diagram. The calculation is relatively straightforward ^[1] and the one-loop result is:

ae=α2π≈0.0011614{displaystyle a_{e}={frac {alpha }{2pi }}approx 0.001;161;4}

where α is the fine structure constant. This result was first found by Julian Schwinger in 1948 ^[2] and is engraved on his tombstone. As of 2016, the coefficients of the QED formula for the anomalous magnetic moment of the electron are known analytically up to α^3 [3] and have been calculated up to order α⁵:^[4][5][6]

ae=0.001159652181643(764){displaystyle a_{e}=0.001;159;652;181;643(764)}

The QED prediction agrees with the experimentally measured value to more than 10 significant figures, making the magnetic moment of the electron the most accurately verified prediction in the history of physics. (See precision tests of QED for details.)

The current experimental value and uncertainty is:^[7]

ae=0.00115965218073(28){displaystyle a_{e}=0.001;159;652;180;73(28)}

According to this value, a_e is known to an accuracy of around 1 part in 1 billion (10⁹). This required measuring g to an accuracy of around 1 part in 1 trillion (10¹²).

Muon

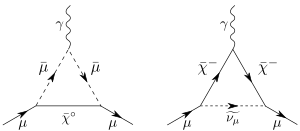
One-loop MSSM corrections to the muon g−2 involving a neutralino and a smuon, and a chargino and a muon sneutrino respectively.

The anomalous magnetic moment of the muon is calculated in a similar way to the electron. The prediction for the value of the muon anomalous magnetic moment includes three parts:^[8]

αμSM=αμQED+αμEW+αμHadron=0.00116591804(51){displaystyle {begin{aligned}alpha _{mu }^{mathrm {SM} }&=alpha _{mu }^{mathrm {QED} }+alpha _{mu }^{mathrm {EW} }+alpha _{mu }^{mathrm {Hadron} }\&=0.001;165;918;04(51)end{aligned}}}

The first two components represent the photon and lepton loops, and the W boson, Higgs boson and Z boson loops, respectively, and can be calculated precisely from first principles. The third term represents hadron loops, and cannot be calculated accurately from theory alone. It is estimated from experimental measurements of the ratio of hadronic to muonic cross sections (R) in electron–antielectron (e⁻e⁺) collisions. As of July 2017, the measurement disagrees with the Standard Model by 3.5 standard deviations,^[9] suggesting physics beyond the Standard Model may be having an effect (or that the theoretical/experimental errors are not completely under control). This is one of the long-standing discrepancies between the Standard Model and experiment.

The E821 experiment at Brookhaven National Laboratory (BNL) studied the precession of muon and antimuon in a constant external magnetic field as they circulated in a confining storage ring.^[10] The E821 Experiment reported the following average value^[8]

aμ=0.0011659209(6).{displaystyle ;a_{mu },=,0.001;165;920;9(6).}

A new experiment at Fermilab called "Muon g−2" using the E821 magnet will improve the accuracy of this value.^[11] Data taking began in 2017 and will continue for three years.^[12]

Tau

Standard Model prediction for tau's anomalous magnetic dipole moment is:

aτ=0.00117721(5){displaystyle a_{tau }=0.001;177;21(5)}

while best measured bound for a_τ is:

−0.007<aτ<0.005{displaystyle -0.007<a_{tau }<0.005}^[13]

Composite particles

Composite particles often have a huge anomalous magnetic moment. This is true for the proton, which is made up of charged quarks, and the neutron, which has a magnetic moment even though it is electrically neutral.

See also

• Anomalous electric dipole moment


• G-factor


• Proton magnetic moment


• Neutron magnetic moment


• Electron magnetic moment

Notes

Bibliography

• 
  Sergei Vonsovsky (1975). Magnetism of Elementary Particles. Mir Publishers.
  

External links

• Overview of the g−2 experiment


• 
  Kusch, P.; Foley, H. M. (1948). "The Magnetic Moment of the Electron". Physical Review. 74 (3): 250–263. Bibcode:1948PhRv...74..250K. doi:10.1103/PhysRev.74.250.