Small stellated 120-cell



















































Small stellated 120-cell

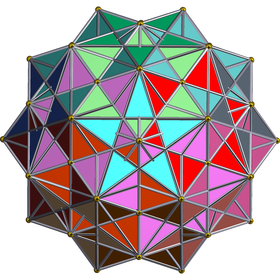Ortho solid 010-uniform polychoron p53-t0.png
Orthogonal projection
Type
Schläfli-Hess polytope
Cells 120 {5/2,5}
Faces 720 {5/2}
Edges 1200
Vertices 120
Vertex figure
{5,3}
Schläfli symbol {5/2,5,3}
Coxeter-Dynkin diagram
CDel node 1.pngCDel 5.pngCDel rat.pngCDel d2.pngCDel node.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node.png
Symmetry group H4, [3,3,5]
Dual
Icosahedral 120-cell
Properties Regular

In geometry, the small stellated 120-cell or stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol {5/2,5,3}. It is one of 10 regular Schläfli-Hess polytopes.




Contents






  • 1 Related polytopes


  • 2 See also


  • 3 References


  • 4 External links





Related polytopes


It has the same edge arrangement as the great grand 120-cell, and also shares its 120 vertices with the 600-cell and eight other regular star 4-polytope. It may also be seen as the first stellation of the 120-cell. In this sense it could be seen as analogous to the three-dimensional small stellated dodecahedron, which is the first stellation of the dodecahedron. Indeed, the small stellated 120-cell is dual to the icosahedral 120-cell, which could be taken as a 4D analogue of the great dodecahedron, dual of the small stellated dodecahedron. With its dual, it forms the compound of icosahedral 120-cell and small stellated 120-cell.


The edges of the small stellated 120-cell are τ2 as long as those of the 120-cell core inside the 4-polytope.

















Orthographic projections by Coxeter planes
H3
 A2 / B3 / D4
 A3 / B2

Small stellated 120-cell ortho-10gon.png
Small stellated 120-cell ortho-6gon.png
Small stellated 120-cell ortho-4gon.png


See also



  • List of regular polytopes


  • Convex regular 4-polytope - Set of convex regular 4-polytope


  • Kepler-Poinsot solids - regular star polyhedron


  • Star polygon - regular star polygons



References




  • Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1].


  • H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
    ISBN 0-486-61480-8.


  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008,
    ISBN 978-1-56881-220-5 (Chapter 26, Regular Star-polytopes, pp. 404–408)


  • Klitzing, Richard. "4D uniform polytopes (polychora) o3o5o5/2x - sishi".



External links



  • Regular polychora

  • Discussion on names

  • Reguläre Polytope

  • The Regular Star Polychora

  • Zome Model of the Final Stellation of the 120-cell

  • The First Stellation of the 120-cell, A Zome Model









-

Popular posts from this blog

Bressuire

Image
Subprefecture and commune in Nouvelle-Aquitaine, France Bressuire Subprefecture and commune Chateau de Bressuire and the Eglise Notre-Dame Coat of arms Location of Bressuire Bressuire Show map of France Bressuire Show map of Nouvelle-Aquitaine Coordinates: 46°50′27″N 0°29′14″W  /  46.8408°N 0.4872°W  / 46.8408; -0.4872 Coordinates: 46°50′27″N 0°29′14″W  /  46.8408°N 0.4872°W  / 46.8408; -0.4872 Country France Region Nouvelle-Aquitaine Department Deux-Sèvres Arrondissement Bressuire Canton Bressuire Government  • Mayor .mw-parser-output .nobold{font-weight:normal} (2014–20) Jean Michel Bernier Area 1 180.59 km 2 (69.73 sq mi) Population (2014) 2 19,300  • Density 110/km 2 (280/sq mi) Time zone UTC+01:00 (CET)  • Summer (DST) UTC+02:00 (CEST) INSEE/Postal code 79049 /79300 Elevation 98–236 m (322–774 ft) (avg. 173 m or 568 ft) 1 French Land Register data, which exclude...
Read more

Vorschmack

Image
Vorschmack Ukrainian Jewish-style vorschmack served on rye bread Course Hors d'oeuvre Region or state Eastern Europe Associated national cuisine Ashkenazi Jewish, Finnish, German, Ukrainian, Polish, Russian Main ingredients Ground meat and/or fish Cookbook: Vorschmack   Media: Vorschmack Vorschmack or forshmak (Yiddish: פֿאָרשמאַק ‎, from archaic German Vorschmack , "foretaste" [1] or "appetizer" [2] ) is an originally East European dish made of salty minced fish or meat. Different variants of this dish are especially common in Ashkenazi Jewish and Finnish cuisine. Some varieties are also known in Russian and Polish cuisine. Contents 1 In Jewish cuisine 2 In Russian cuisine 3 In Polish cuisine 4 In Finnish cuisine 5 See also 6 References In Jewish cuisine According to Gil Marks, the German name points to the possible Germanic origin of this dish. [1] William Pokhlyobkin descr...
Read more

Quarantine

Image
For other uses, see Quarantine (disambiguation). Signal flag "Lima" called the "Yellow Jack" which when flown in harbor means ship is under quarantine. A simple yellow flag (also called the "Yellow Jack") had historically been used to signal quarantine (it stands for Q among signal flags), but now indicates the opposite, as a signal of a ship free of disease that requests boarding and inspection. A quarantine is used to separate and restrict the movement of people; it is 'a restraint upon the activities or communication of persons or the transport of goods designed to prevent the spread of disease or pests', for a certain period of time. [1] This is often used in connection to disease and illness, such as those who may possibly have been exposed to a communicable disease. [2] The term is often erroneously used to mean medical isolation, which is "to separate ill persons who have a communicable disease from those who are healthy...
Read more