Vfrdtyky

This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations. (June 2012) (Learn how and when to remove this template message)

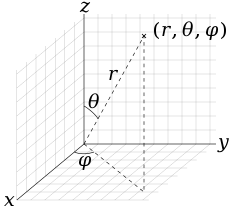
Spherical coordinates (r, θ, φ) as commonly used in physics (ISO convention): radial distance r, polar angle θ (theta), and azimuthal angle φ (phi). The symbol ρ (rho) is often used instead of r.

Spherical coordinates (r, θ, φ) as often used in mathematics: radial distance r, azimuthal angle θ, and polar angle φ. The meanings of θ and φ have been swapped compared to the physics convention.

A globe showing the radial distance, polar angle and azimuth angle of a point P with respect to a unit sphere. In this image, r equals 4/6, θ equals 90°, and φ equals 30°.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.

The radial distance is also called the radius or radial coordinate. The polar angle may be called colatitude, zenith angle, normal angle, or inclination angle.

The use of symbols and the order of the coordinates differs between sources. In one system frequently encountered in physics (r, θ, φ) gives the radial distance, polar angle, and azimuthal angle, whereas in another system used in many mathematics books (r, θ, φ) gives the radial distance, azimuthal angle, and polar angle. In both systems ρ is often used instead of r. Other conventions are also used, so great care needs to be taken to check which one is being used.

A number of different spherical coordinate systems following other conventions are used outside mathematics. In a geographical coordinate system positions are measured in latitude, longitude and height or altitude. There are a number of different celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counterclockwise from the x-axis to the y-axis rather than clockwise from north (0°) to east (+90°) like the horizontal coordinate system.^[1] The polar angle is often replaced by the elevation angle measured from the reference plane. Elevation angle of zero is at the horizon.

The spherical coordinate system generalizes the two-dimensional polar coordinate system. It can also be extended to higher-dimensional spaces and is then referred to as a hyperspherical coordinate system.

Definition

To define a spherical coordinate system, one must choose two orthogonal directions, the zenith and the azimuth reference, and an origin point in space. These choices determine a reference plane that contains the origin and is perpendicular to the zenith. The spherical coordinates of a point P are then defined as follows:

• The radius or radial distance is the Euclidean distance from the origin O to P.


• The inclination (or polar angle) is the angle between the zenith direction and the line segment OP.


• The azimuth (or azimuthal angle) is the signed angle measured from the azimuth reference direction to the orthogonal projection of the line segment OP on the reference plane.

The sign of the azimuth is determined by choosing what is a positive sense of turning about the zenith. This choice is arbitrary, and is part of the coordinate system's definition.

The elevation angle is 90 degrees (π/2 radians) minus the inclination angle.

If the inclination is zero or 180 degrees (π radians), the azimuth is arbitrary. If the radius is zero, both azimuth and inclination are arbitrary.

In linear algebra, the vector from the origin O to the point P is often called the position vector of P.

Conventions

Several different conventions exist for representing the three coordinates, and for the order in which they should be written. The use of (r, θ, φ) to denote radial distance, inclination (or elevation), and azimuth, respectively, is common practice in physics, and is specified by ISO standard 80000-2:2009, and earlier in ISO 31-11 (1992).

However, some authors (including mathematicians) use φ for inclination (or elevation) and θ for azimuth, which "provides a logical extension of the usual polar coordinates notation".^[2] Some authors may also list the azimuth before the inclination (or elevation), and/or use ρ (rho) instead of r for radial distance. Some combinations of these choices result in a left-handed coordinate system. The standard convention (r, θ, φ) conflicts with the usual notation for the two-dimensional polar coordinates, where θ is often used for the azimuth. It may also conflict with the notation used for three-dimensional cylindrical coordinates.
^[2]

The angles are typically measured in degrees (°) or radians (rad), where 360° = 2π rad. Degrees are most common in geography, astronomy, and engineering, whereas radians are commonly used in mathematics and theoretical physics. The unit for radial distance is usually determined by the context.

When the system is used for physical three-space, it is customary to use positive sign for azimuth angles that are measured in the counter-clockwise sense from the reference direction on the reference plane, as seen from the zenith side of the plane. This convention is used, in particular, for geographical coordinates, where the "zenith" direction is north and positive azimuth (longitude) angles are measured eastwards from some prime meridian.

Major conventions

coordinates	corresponding local geographical directions (Z, X, Y)	right/left-handed
(r, θinc, φaz,right)	(U, S, E)	right
(r, φaz,right, θel)	(U, E, N)	right
(r, θel, φaz,right)	(U, N, E)	left

Note: easting (E), northing (N), upwardness (U). Local azimuth angle would be measured, e.g., counterclockwise from S to E in the case of (U, S, E).

Unique coordinates

Any spherical coordinate triplet (r, θ, φ) specifies a single point of three-dimensional space. On the other hand, every point has infinitely many equivalent spherical coordinates. One can add or subtract any number of full turns to either angular measure without changing the angles themselves, and therefore without changing the point. It is also convenient, in many contexts, to allow negative radial distances, with the convention that (−r, θ, φ) is equivalent to (r, θ + 180°, φ) for any r, θ, and φ. Moreover, (r, −θ, φ) is equivalent to (r, θ, φ + 180°).

If it is necessary to define a unique set of spherical coordinates for each point, one must restrict their ranges. A common choice is:

r ≥ 0

0° ≤ θ ≤ 180° (π rad)

0° ≤ φ < 360° (2π rad)

However, the azimuth φ is often restricted to the interval (−180°, +180°], or (−π, +π] in radians, instead of [0, 360°). This is the standard convention for geographic longitude.

The range [0°, 180°] for inclination is equivalent to [−90°, +90°] for elevation (latitude).

Even with these restrictions, if θ is 0° or 180° (elevation is 90° or −90°) then the azimuth angle is arbitrary; and if r is zero, both azimuth and inclination/elevation are arbitrary. To make the coordinates unique, one can use the convention that in these cases the arbitrary coordinates are zero.

Plotting

To plot a dot from its spherical coordinates (r, θ, φ), where θ is inclination, move r units from the origin in the zenith direction, rotate by θ about the origin towards the azimuth reference direction, and rotate by φ about the zenith in the proper direction.

Applications

The geographic coordinate system uses the azimuth and elevation of the spherical coordinate system to express locations on Earth, calling them respectively longitude and latitude. Just as the two-dimensional Cartesian coordinate system is useful on the plane, a two-dimensional spherical coordinate system is useful on the surface of a sphere. In this system, the sphere is taken as a unit sphere, so the radius is unity and can generally be ignored. This simplification can also be very useful when dealing with objects such as rotational matrices.

Spherical coordinates are useful in analyzing systems that have some degree of symmetry about a point, such as volume integrals inside a sphere, the potential energy field surrounding a concentrated mass or charge, or global weather simulation in a planet's atmosphere. A sphere that has the Cartesian equation x² + y² + z² = c² has the simple equation r = c in spherical coordinates.

Two important partial differential equations that arise in many physical problems, Laplace's equation and the Helmholtz equation, allow a separation of variables in spherical coordinates. The angular portions of the solutions to such equations take the form of spherical harmonics.

Another application is ergonomic design, where r is the arm length of a stationary person and the angles describe the direction of the arm as it reaches out.

The output pattern of an industrial loudspeaker shown using spherical polar plots taken at six frequencies

Three dimensional modeling of loudspeaker output patterns can be used to predict their performance. A number of polar plots are required, taken at a wide selection of frequencies, as the pattern changes greatly with frequency. Polar plots help to show that many loudspeakers tend toward omnidirectionality at lower frequencies.

The spherical coordinate system is also commonly used in 3D game development to rotate the camera around the player's position.

In geography

To a first approximation, the geographic coordinate system uses elevation angle (latitude) in degrees north of the equator plane, in the range −90° ≤ φ ≤ 90°, instead of inclination. Latitude is either geocentric latitude, measured at the Earth's center and designated variously by ψ, q, φ′, φ_c, φ_g or geodetic latitude, measured by the observer's local vertical, and commonly designated φ. The azimuth angle (longitude), commonly denoted by λ, is measured in degrees east or west from some conventional reference meridian (most commonly the IERS Reference Meridian), so its domain is −180° ≤ λ ≤ 180°. For positions on the Earth or other solid celestial body, the reference plane is usually taken to be the plane perpendicular to the axis of rotation.

The polar angle, which is 90° minus the latitude and ranges from 0 to 180°, is called colatitude in geography.

Instead of the radial distance, geographers commonly use altitude above or below some reference surface, which may be the sea level or "mean" surface level for planets without liquid oceans. The radial distance r can be computed from the altitude by adding the mean radius of the planet's reference surface, which is approximately 6,360 ± 11 km (3,952 ± 7 miles) for Earth.

However, modern geographical coordinate systems are quite complex, and the positions implied by these simple formulae may be wrong by several kilometers. The precise standard meanings of latitude, longitude and altitude are currently defined by the World Geodetic System (WGS), and take into account the flattening of the Earth at the poles (about 21 km or 13 miles) and many other details.

In astronomy

In astronomy there are a series of spherical coordinate systems that measure the elevation angle from different fundamental planes. These reference planes are the observer's horizon, the celestial equator (defined by Earth's rotation), the plane of the ecliptic (defined by Earth's orbit around the Sun), the plane of the earth terminator (normal to the instantaneous direction to the Sun), and the galactic equator (defined by the rotation of the Milky Way).

Coordinate system conversions

As the spherical coordinate system is only one of many three-dimensional coordinate systems, there exist equations for converting coordinates between the spherical coordinate system and others.

Cartesian coordinates

The spherical coordinates of a point in the ISO convention (i.e. for physics: radius r, inclination θ, azimuth φ) can be obtained from its Cartesian coordinates (x, y, z) by the formulae

r=x2+y2+z2θ=arccos⁡zx2+y2+z2=arccos⁡zrφ=arctan⁡yx{displaystyle {begin{aligned}r&={sqrt {x^{2}+y^{2}+z^{2}}}\theta &=arccos {frac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}=arccos {frac {z}{r}}\varphi &=arctan {frac {y}{x}}end{aligned}}}

The inverse tangent denoted in φ = arctan y/x must be suitably defined, taking into account the correct quadrant of (x,y). See the article on atan2.

Alternatively, the conversion can be considered as two sequential rectangular to polar conversions: the first in the Cartesian xy-plane from (x,y) to (R,φ), where R is the projection of r onto the xy-plane, and the second in the Cartesian zR-plane from (z,R) to (r,θ). The correct quadrants for φ and θ are implied by the correctness of the planar rectangular to polar conversions.

These formulae assume that the two systems have the same origin, that the spherical reference plane is the Cartesian xy-plane, that θ is inclination from the z direction, and that the azimuth angles are measured from the Cartesian x-axis (so that the y-axis has φ = +90°). If θ measures elevation from the reference plane instead of inclination from the zenith the arccos above becomes an arcsin, and the cos θ and sin θ below become switched.

Conversely, the Cartesian coordinates may be retrieved from the spherical coordinates (radius r, inclination θ, azimuth φ), where r ∈ [0, ∞), θ ∈ [0, π], φ ∈ [0, 2π), by:

x=rsin⁡θcos⁡φy=rsin⁡θsin⁡φz=rcos⁡θ{displaystyle {begin{aligned}x&=r,sin theta ,cos varphi \y&=r,sin theta ,sin varphi \z&=r,cos theta end{aligned}}}

Cylindrical coordinates

Cylindrical coordinates (radius ρ, azimuth φ, elevation z) may be converted into spherical coordinates (radius r, inclination θ, azimuth φ), by the formulas

r=ρ2+z2θ=arctan⁡ρz=arccos⁡zρ2+z2φ=φ{displaystyle {begin{aligned}r&={sqrt {rho ^{2}+z^{2}}}\theta &=arctan {frac {rho }{z}}=arccos {frac {z}{sqrt {rho ^{2}+z^{2}}}}\varphi &=varphi end{aligned}}}

Conversely, the spherical coordinates may be converted into cylindrical coordinates by the formulae

ρ=rsin⁡θφ=φz=rcos⁡θ{displaystyle {begin{aligned}rho &=rsin theta \varphi &=varphi \z&=rcos theta end{aligned}}}

These formulae assume that the two systems have the same origin and same reference plane, measure the azimuth angle φ in the same sense from the same axis, and that the spherical angle θ is inclination from the cylindrical z-axis.

Integration and differentiation in spherical coordinates

The following equations assume that θ is inclination from the z (polar) axis (ambiguous since x, y, and z are mutually normal):

The line element for an infinitesimal displacement from (r, θ, φ) to (r + dr, θ + dθ, φ + dφ) is

dr=drr^+rdθθ^+rsin⁡θdφφ^.{displaystyle mathrm {d} mathbf {r} =mathrm {d} r,{hat {mathbf {r} }}+r,mathrm {d} theta ,{hat {boldsymbol {theta }}}+rsin {theta },mathrm {d} varphi ,mathbf {hat {boldsymbol {varphi }}} .}

where

r^=sin⁡θcos⁡φx^+sin⁡θsin⁡φy^+cos⁡θz^θ^=cos⁡θcos⁡φx^+cos⁡θsin⁡φy^−sin⁡θz^φ^=−sin⁡φx^+cos⁡φy^{displaystyle {begin{aligned}{hat {mathbf {r} }}&=sin theta cos varphi ,{hat {mathbf {x} }}+sin theta sin varphi ,{hat {mathbf {y} }}+cos theta ,{hat {mathbf {z} }}\[5px]{hat {boldsymbol {theta }}}&=cos theta cos varphi ,{hat {mathbf {x} }}+cos theta sin varphi ,{hat {mathbf {y} }}-sin theta ,{hat {mathbf {z} }}\[5px]{hat {boldsymbol {varphi }}}&=-sin varphi ,{hat {mathbf {x} }}+cos varphi ,{hat {mathbf {y} }}end{aligned}}}

are the local orthogonal unit vectors in the directions of increasing r, θ, and φ, respectively,
and x̂, ŷ, and ẑ are the unit vectors in Cartesian coordinates.

The general form of the formula to prove the differential line element, is ^[3]

dr=∑i∂r∂xidxi=∑i|∂r∂xi|∂r∂xi|∂r∂xi|dxi=∑i|∂r∂xi|dxix^i{displaystyle mathrm {d} mathbf {r} =sum _{i}{frac {partial mathbf {r} }{partial x_{i}}}mathrm {dx_{i}} =sum _{i}left|{frac {partial mathbf {r} }{partial x_{i}}}right|{frac {frac {partial mathbf {r} }{partial x_{i}}}{left|{frac {partial mathbf {r} }{partial x_{i}}}right|}}mathrm {dx_{i}} =sum _{i}left|{frac {partial mathbf {r} }{partial x_{i}}}right|mathrm {dx_{i}} {hat {boldsymbol {x}}}_{i}}

that is, the change in r{displaystyle {mathbf {r} }} is decomposed into individual changes corresponding to changes in the individual coordinates. To apply this to the present case, you need to calculate how r{displaystyle {mathbf {r} }} changes with each of the coordinates. With the conventions being used, we have

r=[rsin⁡θcos⁡ϕrsin⁡θsin⁡ϕrcos⁡θ]{displaystyle mathbf {r} ={begin{bmatrix}rsin theta cos phi \rsin theta sin phi \rcos theta end{bmatrix}}}

Thus

∂r∂r=[sin⁡θcos⁡ϕsin⁡θsin⁡ϕcos⁡θ],∂r∂θ=[rcos⁡θcos⁡ϕrcos⁡θsin⁡ϕ−rsin⁡θ],∂r∂ϕ=[−rsin⁡θsin⁡ϕrsin⁡θcos⁡ϕ0]{displaystyle {frac {partial mathbf {r} }{partial r}}={begin{bmatrix}sin theta cos phi \sin theta sin phi \cos theta end{bmatrix}},,{frac {partial mathbf {r} }{partial theta }}={begin{bmatrix}rcos theta cos phi \rcos theta sin phi \-rsin theta end{bmatrix}},,{frac {partial mathbf {r} }{partial phi }}={begin{bmatrix}-rsin theta sin phi \rsin theta cos phi \0end{bmatrix}},}

Then the desired coefficients are the magnitudes of these vectors:

|∂r∂r|=1|∂r∂θ|=r|∂r∂ϕ|=rsin⁡θ{displaystyle {begin{aligned}left|{frac {partial mathbf {r} }{partial r}}right|=1\left|{frac {partial mathbf {r} }{partial theta }}right|=r\left|{frac {partial mathbf {r} }{partial phi }}right|=rsin theta \end{aligned}}} ^[4]

The surface element spanning from θ to θ + dθ and φ to φ + dφ on a spherical surface at (constant) radius r is

dSr=‖∂rr^∂θ×∂rr^∂φ‖dθdφ=r2sin⁡θdθdφ.{displaystyle mathrm {d} S_{r}=left|{partial r{hat {mathbf {r} }} over partial theta }times {partial r{hat {mathbf {r} }} over partial varphi }right|mathrm {d} theta ,mathrm {d} varphi =r^{2}sin theta ,mathrm {d} theta ,mathrm {d} varphi .}

Thus the differential solid angle is

dΩ=dSrr2=sin⁡θdθdφ.{displaystyle mathrm {d} Omega ={frac {mathrm {d} S_{r}}{r^{2}}}=sin theta ,mathrm {d} theta ,mathrm {d} varphi .}

The surface element in a surface of polar angle θ constant (a cone with vertex the origin) is

dSθ=rsin⁡θdφdr.{displaystyle mathrm {d} S_{theta }=rsin theta ,mathrm {d} varphi ,mathrm {d} r.}

The surface element in a surface of azimuth φ constant (a vertical half-plane) is

dSφ=rdrdθ.{displaystyle mathrm {d} S_{varphi }=r,mathrm {d} r,mathrm {d} theta .}

The volume element spanning from r to r + dr, θ to θ + dθ, and φ to φ + dφ is (determinant of the Jacobian matrix of partial derivatives):

dV=|∂(x,y,z)∂(r,θ,ϕ)|=r2sin⁡θdrdθdφ=r2drdΩ.{displaystyle mathrm {d} V=left|{frac {partial (x,y,z)}{partial (r,theta ,phi )}}right|=r^{2}sin theta ,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi =r^{2},mathrm {d} r,mathrm {d} Omega .}

Thus, for example, a function f(r, θ, φ) can be integrated over every point in ℝ³ by the triple integral

 ∫φ=02π ∫θ=0π ∫r=0∞f(r,θ,φ)r2sin⁡θdrdθdφ.{displaystyle int limits _{varphi =0}^{2pi } int limits _{theta =0}^{pi } int limits _{r=0}^{infty }f(r,theta ,varphi )r^{2}sin theta ,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi .}

The del operator in this system leads to the following expressions for gradient, divergence, curl and Laplacian:

∇f=∂f∂rr^+1r∂f∂θθ^+1rsin⁡θ∂f∂φφ^,∇⋅A=1r2∂∂r(r2Ar)+1rsin⁡θ∂∂θ(sin⁡θAθ)+1rsin⁡θ∂Aφ∂φ,∇×A=1rsin⁡θ(∂∂θ(Aφsin⁡θ)−∂Aθ∂φ)r^+1r(1sin⁡θ∂Ar∂φ−∂∂r(rAφ))θ^+1r(∂∂r(rAθ)−∂Ar∂θ)φ^,∇2f=1r2∂∂r(r2∂f∂r)+1r2sin⁡θ∂∂θ(sin⁡θ∂f∂θ)+1r2sin2⁡θ∂2f∂φ2=(∂2∂r2+2r∂∂r)f+1r2sin⁡θ∂∂θ(sin⁡θ∂∂θ)f+1r2sin2⁡θ∂2∂φ2f.{displaystyle {begin{aligned}nabla f={}&{partial f over partial r}{hat {mathbf {r} }}+{1 over r}{partial f over partial theta }{hat {boldsymbol {theta }}}+{1 over rsin theta }{partial f over partial varphi }{hat {boldsymbol {varphi }}},\[8pt]nabla cdot mathbf {A} ={}&{frac {1}{r^{2}}}{partial over partial r}left(r^{2}A_{r}right)+{frac {1}{rsin theta }}{partial over partial theta }left(sin theta A_{theta }right)+{frac {1}{rsin theta }}{partial A_{varphi } over partial varphi },\[8pt]nabla times mathbf {A} ={}&{frac {1}{rsin theta }}left({partial over partial theta }left(A_{varphi }sin theta right)-{partial A_{theta } over partial varphi }right){hat {mathbf {r} }}\[8pt]&{}+{frac {1}{r}}left({1 over sin theta }{partial A_{r} over partial varphi }-{partial over partial r}left(rA_{varphi }right)right){hat {boldsymbol {theta }}}\[8pt]&{}+{frac {1}{r}}left({partial over partial r}left(rA_{theta }right)-{partial A_{r} over partial theta }right){hat {boldsymbol {varphi }}},\[8pt]nabla ^{2}f={}&{1 over r^{2}}{partial over partial r}left(r^{2}{partial f over partial r}right)+{1 over r^{2}sin theta }{partial over partial theta }left(sin theta {partial f over partial theta }right)+{1 over r^{2}sin ^{2}theta }{partial ^{2}f over partial varphi ^{2}}\[8pt]={}&left({frac {partial ^{2}}{partial r^{2}}}+{frac {2}{r}}{frac {partial }{partial r}}right)f+{1 over r^{2}sin theta }{partial over partial theta }left(sin theta {frac {partial }{partial theta }}right)f+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}f.end{aligned}}}

Kinematics

In spherical coordinates the position of a point is written

r=rr^.{displaystyle mathbf {r} =rmathbf {hat {r}} .}

Its velocity is then

v=r˙r^+rθ˙θ^+rφ˙sin⁡θφ^,{displaystyle mathbf {v} ={dot {r}}mathbf {hat {r}} +r,{dot {theta }},{hat {boldsymbol {theta }}}+r,{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {varphi }}} ,}

and its acceleration is

a=(r¨−rθ˙2−rφ˙2sin2⁡θ)r^+(rθ¨+2r˙θ˙−rφ˙2sin⁡θcos⁡θ)θ^+(rφ¨sin⁡θ+2r˙φ˙sin⁡θ+2rθ˙φ˙cos⁡θ)φ^.{displaystyle {begin{aligned}mathbf {a} &=left({ddot {r}}-r,{dot {theta }}^{2}-r,{dot {varphi }}^{2}sin ^{2}theta right)mathbf {hat {r}} \&{}+left(r,{ddot {theta }}+2{dot {r}},{dot {theta }}-r,{dot {varphi }}^{2}sin theta cos theta right){hat {boldsymbol {theta }}}\&{}+left(r{ddot {varphi }},sin theta +2{dot {r}},{dot {varphi }},sin theta +2r,{dot {theta }},{dot {varphi }},cos theta right){hat {boldsymbol {varphi }}}.end{aligned}}}

In the case of a constant φ or θ = π/2, this reduces to vector calculus in polar coordinates.

See also

• Celestial coordinate system


• Del in cylindrical and spherical coordinates


• Elevation (ballistics)


• Euler angles


• Gimbal lock


• Hypersphere


• Jacobian matrix and determinant


• List of canonical coordinate transformations


• Sphere


• Spherical harmonic


• Theodolite


• Vector fields in cylindrical and spherical coordinates


• Yaw, pitch and roll

Notes

Bibliography

• 
  Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 658. ISBN 0-07-043316-X. LCCN 52011515.
  


• 
  Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 177–178. LCCN 55010911.
  


• 
  Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. pp. 174–175. LCCN 59014456. ASIN B0000CKZX7.
  


• 
  Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 95–96. LCCN 67025285.
  


• 
  Moon P, Spencer DE (1988). "Spherical Coordinates (r, θ, ψ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 24–27 (Table 1.05). ISBN 978-0-387-18430-2.
  


• 
  Duffett-Smith P, Zwart J (2011). Practical Astronomy with your Calculator or Spreadsheet, 4th Edition. New York: Cambridge University Press. p. 34. ISBN 978-0521146548.
  

External links

• 
  Hazewinkel, Michiel, ed. (2001) [1994], "Spherical coordinates", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
  


• MathWorld description of spherical coordinates


• Coordinate Converter — converts between polar, Cartesian and spherical coordinates


• 
  Conventions for Spherical Coordinates Description of the different conventions in use for naming components of spherical coordinates, along with a proposal for standardizing this.